'S(I)alem's Lot
Caution Constant Readers! This post contains spoilers for Stephen King’s second published novel, ‘Salem’s Lot.
Since we're right in the time of ghouls, goblins, werewolves, and vampires, I wanted to revisit one of my favorite Stephen King novels—and recently released Max original film—‘Salem’s Lot. When I first read this book, it was striking how much the spread of vampirism resembled the spread of an infectious disease. My academic background is in mathematical epidemiology, so I thought it would be fun to model Jerusalem's Lot's turn.
From Stephen King to mathematical epidemiology
"They're breeding on one another. The vampires are creating vampires. It's a geometric progression.
Two times two... ...times four, times eight."
-Ben Mears, 'Salem's Lot (1979 Mini Series).
In 'Salem's Lot, vampirisim follows the classic vampire rules: vampire bites person, person dies, comes back as a vampire, then starts biting people themselves. There is no recovery. Once you're a vampire, you're a vampire until someone else kills you.
We might try analyzing this spread not with a geometric growth model but with an \(SI\) model1 (which is equivalent to logistic growth). The \(S\) in \(SI\) stands for susceptible, indicating people in the population who are not immune from the disease, while \(I\) stands for infected, people who have the disease and can spread it to the susceptible. People flow from the susceptible population to the infected population at some rate. Here we assume that there is no way to recover from the disease and that an infected person is forever infectious.
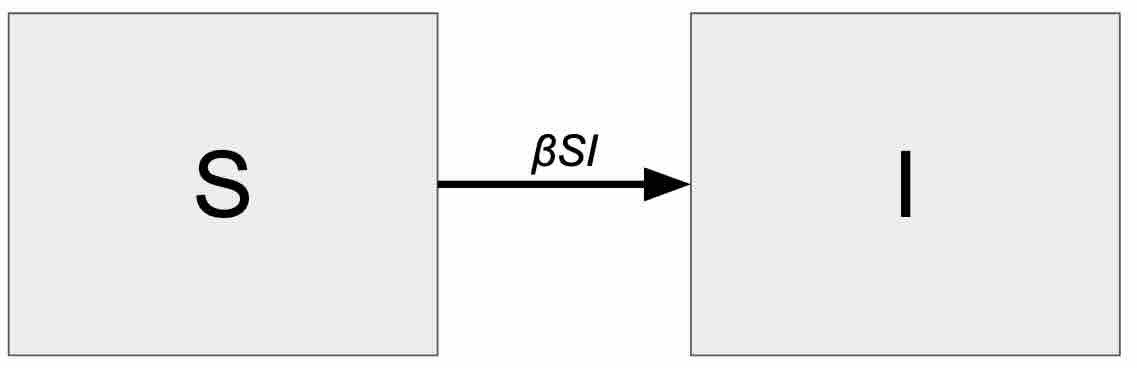
A compartmental diagram of the \(SI\) model showing the flow of the population from susceptibles to infecteds.
We assume the simplest form of this model, one in which there are no new people entering the population (through immigration or birth) and that nobody leaves (through death or emigration). While there is some migration in the story, for example, Ben Mears returning to the Lot at the beginning of the book, I would argue that it has negligible impact on the population dynamics of Jerusalem’s Lot over the course of the book.
Getting disease progression data from a novel
“The town has a sense, not of history, but of time, and the telephone poles seem to know this. If you lay your hand against
one, you can feel the vibration from the wires deep within the wood, as if souls had been imprisoned in there and were
struggling to get out.”
―Stephen King, ’Salem’s Lot
Throughout ‘Salem’s Lot, King wields an accelerating clock to build suspense. His use of time makes for both a thrilling experience for the general audience and an informative experience for the public health audience.
Vampire:
Appears:
Book Quote:
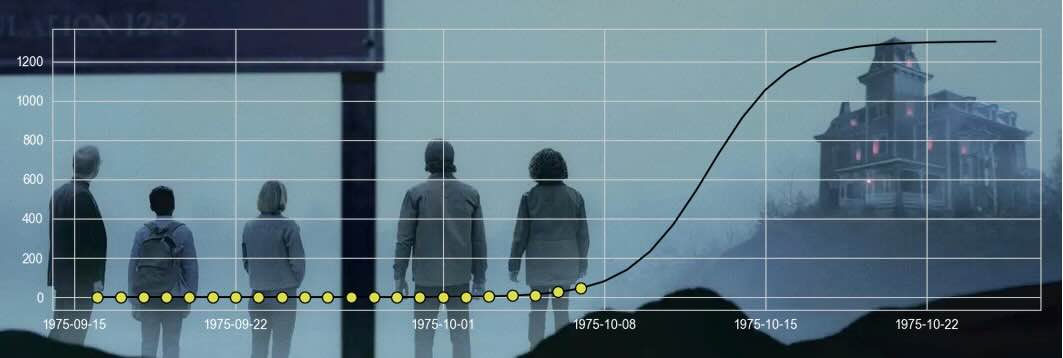
The text allows us to extract day-level data for each vampiric “infection”, as can be seen in the chart above. This gives us the number of vampires at the end of each day, which is known as the vampiric prevalence in public health terms. We can in turn use this data to fit the \(SI\) model, written below.
\(\frac{dS}{dt} = -\frac{\beta}{N} S I\), \(\frac{dI}{dt} = \frac{\beta}{N} S I,\) so
\( I = \frac{D e^{\beta t}}{1 + \frac{D}{N} e^{\beta t}} \),
Where \( N\) is the population of the Lot, and \( \beta \) and \( D \) are parameters we need to estimate.
We will use the novel's population size, 1300, stated by Susan in her first encounter with Ben. A grid search that minimized the mean squared error gave estimates of \( \hat{\beta} = 0.595, \ \hat{D} = 1.37 \times 10^{-7} \).
Pronouncing the Lot (un)dead
"No one pronounced Jerusalem’s Lot dead on the morning of October 6; no one knew it was. Like the bodies of
previous days, it retained every semblance of life."
-Stephen King, ’Salem’s Lot
The narrator of 'Salem's Lot pronounces the Lot dead on the morning of October 6, but from the information provided to the reader, only 27 of the town's 1300 residents had turned by that point. The results of our \(SI\) model2 would pronounce the town (un)dead by the end of October 1975 as shown in the plot below.
That quote does not suggest that all of the town's residents are now vampires, but rather it conveys that the town's fate is sealed on October 6, 1975. The question of the story then becomes whether our intrepid heroes can save themselves and avenge their loved ones. With a non-paranormal infectious disease, two percent of the population being infected might be manageable, especially when we consider that our characters were aware of the mode of transmission. In this setting, however, it would take a considerable force to take out 27 vampires and prevent future spread. Further, King has made it quite clear that the Lot is not the type of town that bands together to oust evil, even while it is sucking on their necks.
Notes
1. There are actually a few different model types you could consider
for the "outbreak" depicted in this novel. For example, an \(SEI\) model would be reasonable since some people were
exposed to a vampire, but did not turn for a few days. These people would not be susceptible nor infected and
might warrant their own compartment. The data presented in the book would have made fitting such a model impossible. We
could also have used a much more complicated model with multiple infected compartments based on the idea of different
vampire types that King presented in his Dark Tower series, but since this novel was written well before that concept was
introduced, I think our simple \(SI\) model works just fine.
2. There are many assumptions for the \(SI\) model that this post
is sweeping under the rug. For example, compartmental models assume homogeneous mixing patterns, meaning everyone in
the population is equally likely to contact anyone else in the population. This may not be true here; however, a
small town cliche is that everybody knows everybody else, which King demonstrates several times throughout the pre-vampire
portion of the story. Applying a model with more strict assumptions would probably decrease the speed of the spread. I
think that, if anything, Stephen King may think that the spreading speed exhibited by the model isn't fast enough!