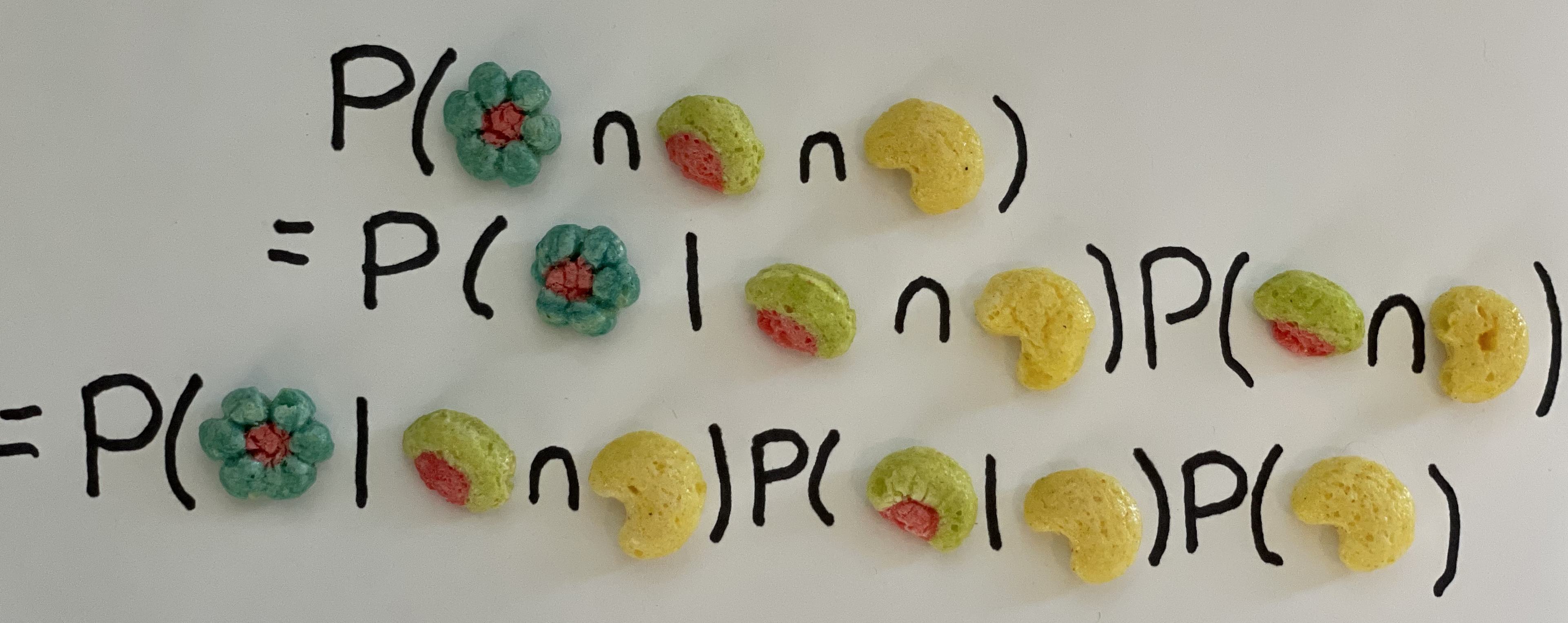Good Morning!

After listening to our new favorite meditative cereal podcast, The Empty Bowl, my girlfriend and I got nostalgic for the Saturday mornings of yore and bought a box of that silly Rabbit's favorite breakfast cereal, Trix. As I was waiting for the bagel accompanying that delectable bowl of fruity goodness I looked at the back of the box to check out the fun diversion cooked up by the geniuses over at General Mills.

For those of you having a difficult time reading the box from my cell phone picture, let me give you the run down on the high stakes world of Trix Rabbit Racer. You start on the red race car and draw a piece of cereal at random from the box and then move to the closest circle containing the shape you have pulled. If you are able to travel all the way down to the Finish Circle in seven pulls or less, Congratulations! You have beaten Tricks the Trix rabbit in a race.

Now my toaster is old, and it takes a long time to toast a bagel so I played a couple times.

This. Game. Is. Hard.

I quickly saw that there seems to only be a few possible pull combinations that result in a win. I was infuriated, why would these monsters make a game FOR CHILDREN so difficult to win? This faux rage pulled me down a rabbit hole of probability theory. That's right, I actually sat down and did the math. The probability that someone could win this race with Tricks the Trix rabbit is *SPOILER ALERT* less than 3%.

If you aren't especially interested with seeing how I calculated that result click here to go to the end of this post and play Trix Rabbit Racer yourself!

The Math

In order to calculate the probability all we need to do is find the probability of getting a particular draw and then sum up the probabilities associated with winning routes.

There are six deliciously fruity shapes inside a box of Trix: Watermelon, Raspberry Red, Wildberry Blue, Banana, Orangey Orange, and Grapity Purple. This means that there are \(6^7 = 279{,}936\) possible draws of \(7\) cereal bits when playing this game.

To calculate the probability of each one of those draws we have to make some assumptions. For one, let's assume that at the begining of the game each shape is present in the box in equal amounts. Let's also assume that your box is full. What is more exhilirating than opening a fresh box of sugar cereal? We now have two paths forward, we can live in reality where cereal boxes are finite, or we can live in a fantasy land where the Trix never stop flowing.

Infinite Trix

As Homer Simpson might say, "Mmmmmmmmm.... Infinite Trix.... *mouth watering noises*".

The assumption of an infinite box when combined with the assumption of a uniform distribution of fruity shapes makes our lives a little easier. In this setting we can assume that drawing one shape will have no impact on the next draw, i.e. each draw is independent of all others. Thus every possible collection of seven draws will be equally likely, so we just need to count up the total winning paths and divide by \(279{,}936\) to get the probability that you will win.

Using the help of Python, I have found that only \(7{,}095\) paths result in a win. And so under the assumption of an infinite box the probability that you will win a game is about \(2.5345\%\).

A Finite Box

Back to reality, oops there goes... infinite Trix. Let's take a look at a more realistic setting.

With a finite box, we can no longer assume that the first draw does not impact the second draw. However, we can use conditional probability to calculate the probability of a certain set of seven draws. Recall that for two events \(A\) and \(B\) it holds that \( P(A \cap B) = P(A | B) P (B) \). So if we consider just two draws, we have that: \[{ P(\{\text{Draw 2}=b\} \cap \{\text{Draw 1} = a\}) = P(\text{Draw 2}=b \ | \ \text{Draw 1} = a) P(\text{Draw 1} = a). }\] This can be applied repeatedly for a set of seven consecutive draws.

All we need to figure out the probability is an estimate of how many fruity bits are in a single box of Trix. To figure this out I weighed \(20\) pieces of each shape on a kitchen scale. All of my measurements came out to \(3\) grams, which translates to \(3/20\) grams per piece for each of the six shapes. According to the Nutritional Facts on my box there are about \(312\) grams of cereal in the box. This translates to \(2080\) individual pieces of cereal in a box of Trix, but we'll be generous and round this up to \(2082\) which is divisible by \(6\). Thus at the begining of our game of Trix Rabbit Racer the box will have \(347\) pieces of each fun fruity shape. Now we can calculate some probabilities.

To save writing let's demonstrate how I did this with calculating the probability of a series of three pulls resulting in say, Watermelon, Grapity Purple and Watermelon. \[{ P(\text{Watermelon} \cap \text{Grapity Purple} \cap \text{Watermelon})}\] \[{= P(\text{Watermelon} \ | \ \text{Grapity Purple} \cap \text{Watermelon}) \times P(\text{Grapity Purple} \cap \text{Watermelon}) }\] \[{=P(\text{Watermelon} \ | \ \text{Grapity Purple} \cap \text{Watermelon}) \times P(\text{Grapity Purple} | \text{Watermelon}) \times P(\text{Watermelon}) }\] \[{ = \frac{346}{2080} \times \frac{347}{2081} \times \frac{347}{2082} }\] We can do this for all \(279{,}936\) possible paths and just add up the resulting probabilities for those where we win. Doing so gives that the probability you would win a round of Trix Rabbit Racer using an average box of Trix as \(2.5306\%\). Looks like all that extra work for the finite box didn't make much of a difference!

Start Your Engines!

I couldn't end this post without giving you the ability to try your hand at Trix Rabbit Racer. Below you can draw a piece (from either an infinite or finite box of Trix) one at a time and see the updated probability of winning the race. Click "Draw" to draw a new shape, and click "New Race" when you get enraged enough to play again.

Big Cereal?

Is this devilishly difficult drag race a plot by General Mills to trick kids into eating more Trix cereal? Perhaps...

But it's probably far more likely that the people who designed the game didn't think too hard about the probability of a child actually winning this game. I browsed their other back-of-the-box games and this appeared to be the only one with a game of chance. There may even be something to say about the sense of accomplishment that winning this race instills in our youth.

However... if I go missing shortly after this post goes up maybe start the investigation with Tricks the Trix Rabbit.